프림 최소 스패닝 트리
도입
스패닝 트리
보통 '신장 트리' 라고 알려진 이 트리 형태는 사이클이 없고 모든 정점이 연결된 형태의 트리이다.
대표적으로 크루스칼, 프림 2가지 방식이 있는데 여기서는 프림만 다룬다.
크루스칼 알고리즘은 여기저기 만들어진 트리 조각들을 합쳐서 스패닝 트리를 만드는 반면, 프림 알고리즘은 하나의 시작점으로 구성된 트리에 간선을 추가하는 방식이다.
시간 복잡도
그냥 단순히 정점을 추가할 때 마다 간선을 검색한다면 $O(|E||V|)$ 의 시간 복잡도를 갖으나,
최적화를 통해 $O(|V|^2+|E|)$ 가 될 수 있다.
알고리즘
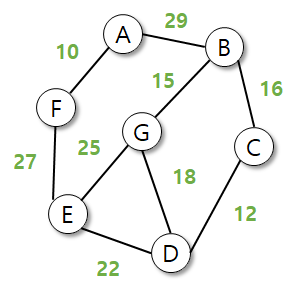
- 시작점을 기준으로 트리에 추가할 정점을 추가
- 기존 트리에 존재하지 않으면서, 가중치가 가장 작은 간선 선택
- 선택된 정점으로부터 기존 정점(u)까지 최저비용 갱신
사이클이 생기는 것을 어떻게 판단하는가?
-> 이미 방문한 지점을 저장
동작 과정은 다음과 같다.



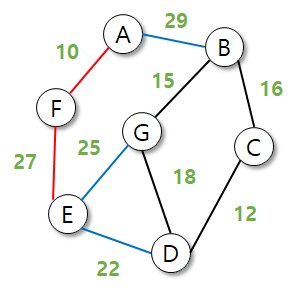
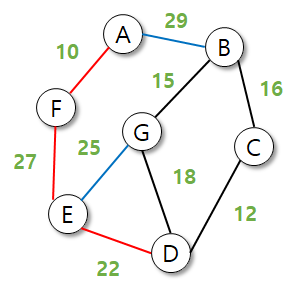


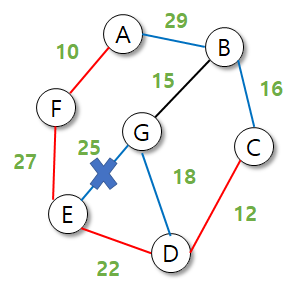
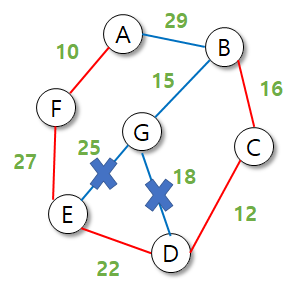
프림 알고리즘의 최적화의 가장 중요한 부분이다.
이미 E로 가는 간선이 있기 때문에 G->E로 가는 비용이 더 크면 선택할 일이 없다.
따라서 G에서 다른 최소 간선과 잇는 것이 최소비용을 반환하므로 25를 후보에서 제거한다.
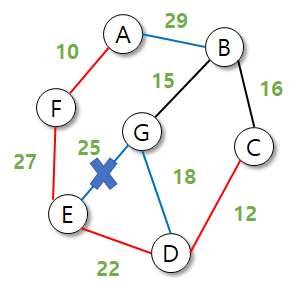



코드
import java.util.Vector;
public class 프림_최소_스패닝_트리 {
// 정점의 최대 갯수를 MAX_V로 저장
final static int MAX_V = 100;
// 엄청 큰 값
final static int INF = 987654321;
// 정점의 개수
static int V;
// 가중치 그래프 저장용 클래스
static class Pair<A, B> {
A first;
B second;
public Pair(A first, B second) {
this.first = first;
this.second = second;
}
}
// 그래프의 인접 리스트. (연결된 정점 번호, 간선 가중치)쌍을 담는다.
static Vector<Vector<Pair<Integer, Integer>>> adj;
static int Prim(Vector<Pair<Integer, Integer>> selected) {
selected.clear();
// 정점의 갯수만큼 added를 false로 초기화
Vector<Boolean> added = new Vector<>(V);
for (int i = 0; i < V; i++) {
added.add(false);
}
//
Vector<Integer> minWeight = new Vector<>(V);
for (int i = 0; i < V; i++) {
minWeight.add(INF);
}
Vector<Integer> parent = new Vector<>(V);
for (int i = 0; i < V; i++) {
parent.add(-1);
}
// 가중치의 합을 저장할 변수
int ret = 0;
// 0번 정점을 시작점으로 항상 트리에 가장 먼저 추가
minWeight.set(0, 0);
parent.set(0, 0);
for (int i = 0; i < V; i++) {
// 다음에 트리에 추가할 정점 u를 찾는다.
int u = -1;
for (int v = 0; v < V; v++) {
// v가 선택된 정점이 아니고,
// 최초 반복이거나
// 기존 u에 저장된 weight값이 v의 weight값 보다 크면
if (!added.get(v) && (u == -1 || minWeight.get(u) > minWeight.get(v))) {
u = v;
}
}
// parent.get(u),u를 트리에 추가
if (parent.get(u) != u) {
selected.add(new Pair<Integer, Integer>(parent.get(u), u));
}
ret += minWeight.get(u);
added.set(u, true);
// u에 인접한 간선 (u,v)를 검사한다.
for (int j = 0; j < adj.get(u).size(); j++) {
int v = adj.get(u).get(j).first;
int weight = adj.get(u).get(j).second;
if (!added.get(v) && minWeight.get(v) > weight) {
parent.set(v, u);
minWeight.set(v, weight);
}
}
}
return ret;
}
// 정점에 닿는 최소 간선의 정보를 저장
public static void main(String[] args) {
// 초기화
adj = new Vector<>();
// 정점의 수
V = 7;
// 정점의 수 만큼 삽입
for (int i = 0; i < 7; i++) {
adj.add(new Vector<>());
}
// A<->B
adj.get(0).add(new Pair<Integer, Integer>(1, 29));
adj.get(1).add(new Pair<Integer, Integer>(0, 29));
// A<->F
adj.get(0).add(new Pair<Integer, Integer>(5, 10));
adj.get(5).add(new Pair<Integer, Integer>(0, 10));
// B<->C
adj.get(1).add(new Pair<Integer, Integer>(2, 16));
adj.get(2).add(new Pair<Integer, Integer>(1, 16));
// B<->G
adj.get(1).add(new Pair<Integer, Integer>(6, 15));
adj.get(6).add(new Pair<Integer, Integer>(1, 15));
// C<->D
adj.get(2).add(new Pair<Integer, Integer>(3, 12));
adj.get(3).add(new Pair<Integer, Integer>(2, 12));
// D<->E
adj.get(3).add(new Pair<Integer, Integer>(4, 22));
adj.get(4).add(new Pair<Integer, Integer>(3, 22));
// D<->G
adj.get(3).add(new Pair<Integer, Integer>(6, 18));
adj.get(6).add(new Pair<Integer, Integer>(3, 18));
// E<->F
adj.get(4).add(new Pair<Integer, Integer>(5, 27));
adj.get(5).add(new Pair<Integer, Integer>(4, 27));
// E<->G
adj.get(4).add(new Pair<Integer, Integer>(6, 25));
adj.get(6).add(new Pair<Integer, Integer>(4, 25));
Vector<Pair<Integer, Integer>> selected = new Vector<>();
int ret = Prim(selected);
System.out.println(ret);
for (int i = 0; i < selected.size(); i++) {
System.out.println((char) (selected.get(i).first + 65) + " " + (char) (selected.get(i).second + 65) + "선택");
}
}
}출력
102
A F선택
F E선택
E D선택
D C선택
C B선택
B G선택'Algorithm > 알고리즘 (Java)' 카테고리의 다른 글
| [Java] DFS : 깊이 우선 탐색 (0) | 2021.12.01 |
|---|---|
| [Java] 트라이(Trie) 알고리즘 (0) | 2021.11.16 |
| [Java] 상호 배타적 집합 (0) | 2021.09.23 |
| [Java] 크루스칼 최소 스패닝 트리 (0) | 2021.09.23 |
| [Java] 위상정렬 알고리즘 (0) | 2021.09.13 |
![[Java] 프림 최소 스패닝 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FrIU6m%2Fbtrk7tnbc0z%2FAAAAAAAAAAAAAAAAAAAAALs8jp04wwRVx2c3Drqkn2gf2rkE7fd5P2HsO5q-SWzm%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DbsE03B7%252B1dJB%252FDtWv2wSbjeHyoU%253D)