크루스칼 최소 스패닝 트리
도입
스패닝 트리
보통 '신장 트리' 라고 알려진 이 트리 형태는 사이클이 없고 모든 정점이 연결된 형태의 트리이다.
대표적으로 크루스칼, 프림 2가지 방식이 있는데 여기서는 크루스칼만 다룬다.
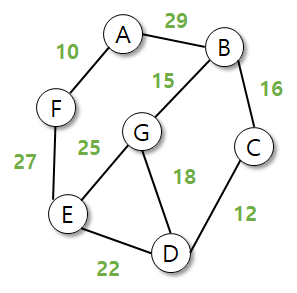
알고리즘
- 모든 간선을 가중치의 오름차순으로 정렬
- 간선을 트리에 추가 (단, 사이클이 생기는 간선은 고려 제외)
사이클이 생기는 것을 어떻게 판단하는가?
-> 상호 배타적 집합 자료구조 사용
동작 과정은 다음과 같다.




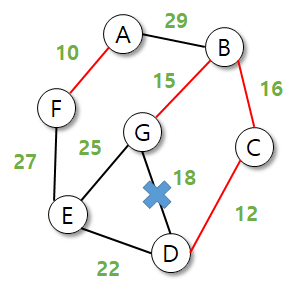


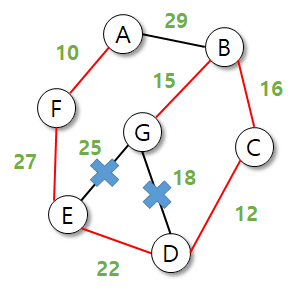

코드
import java.util.Comparator;
import java.util.Vector;
public class 크루스칼_최소_스패닝_트리 {
static class DisjointSet {
// parent : 각 노드의 부모 위치
Vector<Integer> parent;
// rank : 각 노드의 높이
Vector<Integer> rank;
public DisjointSet(int n) {
parent = new Vector<>();
rank = new Vector<>();
// 노드 수 만큼 반복
for (int i = 0; i < n; i++) {
// 처음은 자기 자신이 부모
parent.add(i);
// 높이는 1로 초기화
rank.add(1);
}
}
// u가 속한 트리의 루트 번호를 반환한다.
public int find(int u) {
// 루트 번호면 자기 자신이므로 끝남.
if (u == parent.get(u))
return u;
// 루트 번호 갱신
int ret = find(parent.get(u));
parent.set(u, ret);
return ret;
}
// u가 속한 트리와 v가 속한 트리를 합친다.
public void merge(int u, int v) {
// u, v 의 각각 루트 노드 구하기
u = find(u);
v = find(v);
// u, v 가 같은 트리에 속한다면...
// 바로 종료
if (u == v)
return;
// u의 깊이가 v보다 깊다면..
// v뒤에 u를 붙이자!
if (rank.get(u) > rank.get(v)) {
int tmp = u;
u = v;
v = tmp;
}
// u의 루트를 v루트 뒤에 붙인다.
parent.set(u, v);
if (rank.get(u) == rank.get(v)) {
rank.set(v, rank.get(v) + 1);
}
}
}
static class Pair<A, B> {
A first;
B second;
public Pair(A first, B second) {
this.first = first;
this.second = second;
}
}
final static int MAX_V = 100;
// 정점의 개수
static int V;
// 그래프의 인접 리스트
static Vector<Vector<Pair<Integer, Integer>>> adj;
//
public static int kruskal(Vector<Pair<Integer, Integer>> selected) {
// 가중치의 합 저장
int ret = 0;
selected.clear();
Vector<Pair<Integer, Pair<Integer, Integer>>> edges = new Vector<>();
// <비용 <from, to>> 데이터화
for (int u = 0; u < V; u++) {
for (int i = 0; i < adj.get(u).size(); i++) {
int v = adj.get(u).get(i).first, cost = adj.get(u).get(i).second;
edges.add(new Pair<Integer, Pair<Integer, Integer>>(cost, new Pair<Integer, Integer>(u, v)));
}
}
// edges를 가중치 순으로 정렬
edges.sort(new Comparator<Pair<Integer, Pair<Integer, Integer>>>() {
@Override
public int compare(Pair<Integer, Pair<Integer, Integer>> o1, Pair<Integer, Pair<Integer, Integer>> o2) {
// TODO Auto-generated method stub
return o1.first - o2.first;
}
});
// 상호 배타적 집합 자료구조 사용
DisjointSet sets = new DisjointSet(V);
System.out.println("edge 사이즈 : " + edges.size());
for (int i = 0; i < edges.size(); i++) {
// 비용, from, to 데이터 추출
int cost = edges.get(i).first;
int u = edges.get(i).second.first, v = edges.get(i).second.second;
// 이미 연결되어 있는 경우 무시
if (sets.find(u) == sets.find(v))
continue;
// 이 둘을 합친다.
sets.merge(u, v);
selected.add(new Pair<Integer, Integer>(u, v));
ret += cost;
}
return ret;
}
public static void main(String[] args) {
// 초기화
adj = new Vector<>();
// 정점의 수
V = 10;
// 정점의 수 만큼 삽입
for (int i = 0; i < 10; i++) {
adj.add(new Vector<>());
}
// A<->B
adj.get(0).add(new Pair<Integer, Integer>(1, 29));
adj.get(1).add(new Pair<Integer, Integer>(0, 29));
// A<->F
adj.get(0).add(new Pair<Integer, Integer>(5, 10));
adj.get(5).add(new Pair<Integer, Integer>(0, 10));
// B<->C
adj.get(1).add(new Pair<Integer, Integer>(2, 16));
adj.get(2).add(new Pair<Integer, Integer>(1, 16));
// B<->G
adj.get(1).add(new Pair<Integer, Integer>(6, 15));
adj.get(6).add(new Pair<Integer, Integer>(1, 15));
// C<->D
adj.get(2).add(new Pair<Integer, Integer>(3, 12));
adj.get(3).add(new Pair<Integer, Integer>(2, 12));
// D<->E
adj.get(3).add(new Pair<Integer, Integer>(4, 22));
adj.get(4).add(new Pair<Integer, Integer>(3, 22));
// D<->G
adj.get(3).add(new Pair<Integer, Integer>(6, 18));
adj.get(6).add(new Pair<Integer, Integer>(3, 18));
// E<->F
adj.get(4).add(new Pair<Integer, Integer>(5, 27));
adj.get(5).add(new Pair<Integer, Integer>(4, 27));
// E<->G
adj.get(4).add(new Pair<Integer, Integer>(6, 25));
adj.get(6).add(new Pair<Integer, Integer>(4, 25));
Vector<Pair<Integer, Integer>> selected = new Vector<>();
int ret = kruskal(selected);
System.out.println(ret);
for (int i = 0; i < selected.size(); i++) {
System.out.println(selected.get(i).first + " " + selected.get(i).second + "선택");
}
}
}
출력
edge 사이즈 : 18
102
0 5 선택
2 3 선택
1 6 선택
1 2 선택
3 4 선택
4 5 선택'Algorithm > 알고리즘 (Java)' 카테고리의 다른 글
| [Java] 프림 최소 스패닝 트리 (0) | 2021.11.15 |
|---|---|
| [Java] 상호 배타적 집합 (0) | 2021.09.23 |
| [Java] 위상정렬 알고리즘 (0) | 2021.09.13 |
| [Java] 다익스트라(Dijkstra) 알고리즘 (0) | 2021.09.06 |
| 8/12 (목) 자바 코딩 스터디 (0) | 2021.08.14 |
![[Java] 크루스칼 최소 스패닝 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F1SV6y%2FbtrfMNSIKwI%2FAAAAAAAAAAAAAAAAAAAAAJyfx3fOfymlRu27L4epv8ViI0bzZeV9P_qOtGi5WpIH%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DxcRmEx9FqLyLFc6WUWw44KDnmD0%253D)