분할 정복 알고리즘

도입

분할 정복과 일반적 재귀 호출의 차이

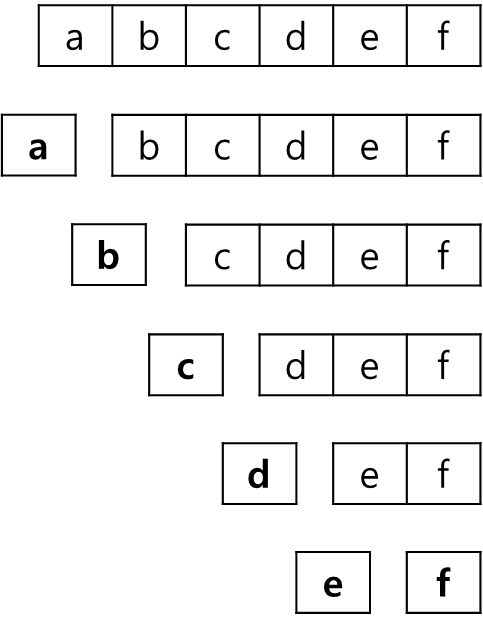
일반적 재귀 호출

문제를 한 조각과 나머지 전체로 나눔

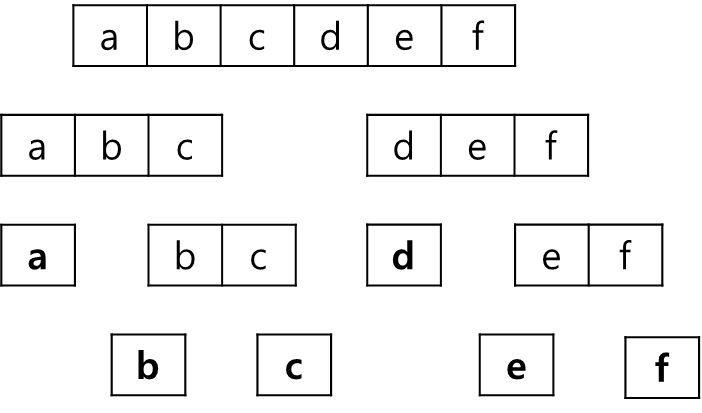
분할정복

문제를 항상 거의 같은 크기로 나눔

일반적 재귀 호출

분할 정복

분할 정복의 구성 요소

• divide
  • 문제를 더 작은 문제로 분할하는 과정

• merge
  • 각 문제에 대해 구한 답을 원래 답으로 병합하는 과정

• base case
  • 매우 작은 문제의 해법

---

예제: 수열의 빠른 합과 행렬의 빠른 제곱

가장 간단한 방법은 수식을 이용하여 바로 계산하는 것이다.

하지만, 우리는 분할 정복 알고리즘에 익숙해지기 위해 이를 이용하여 계산해보자

1+2+…+n 의 합을 분할 정복을 이용하여 계산해보자

문제를 반으로 나눠보기

1부터 $n\over2$까지의 합과 ${n\over2}+1$부터 n까지의 합을 구하는 문제로 나눠보자

$$\begin{aligned} sum(n) &= 1+2+...+n \\ &= (1+2+...+{n\over2})(({n\over2}+1)+...+n) \end{aligned}$$

여기서 ${n\over2}+1$부터 n까지의 합을 살펴보자

$$({n\over2}+1)+...+n = ({n\over2}+1)+({n\over2}+2)+({n\over2}+3)+...+({n\over2}+{n\over2})$$

$n\over2$을 빼서 살펴보면 1부터 $n\over2$까지의 합과 같아진다.

위 식에 $n\over2$가 $n\over2$개 있으므로.. 전체 식을 다시 정리하면 다음과 같다.

$$\begin{aligned} sum(n) &= 2*sum({n\over2})+({n\over2})^2\,(n은\,짝수) \end{aligned}$$

홀수 처리하기

근데 문제는 n이 홀수라면? 어떻게 처리를 할까?

답은 간단하다. sum(n)을 짝수로 만들면 된다.

즉, 식을 다음과 같이 수정하도록 하자

$$sum(n) = n+sum(n-1) \,(n은\,홀수)$$

코드 구현하기

위 알고리즘대로 구현한 코드를 보자

static int fastSum(int n) {
    // n이 1이면 1을 반환한다.
    if (n == 1) {
        return 1;
    }
    // n이 홀수인 경우
    // n을 미리 더하고 짝수로 바꾼다.
    if (n % 2 != 0) {
        return n + fastSum(n - 1);
    }

    return 2 * fastSum(n / 2) + (n / 2) * (n / 2);
}

위와 같이 간단하게 구현이 가능하다.

시간 복잡도

1부터 n까지의 합을 단순한 알고리즘대로 계산하면 $O(n)$만큼의 시간이 걸릴것이다.

하지만 분할 정복을 이용한다면 문제마다 크기가 절반으로 줄어들기 때문에 시간 복잡도는 다음과 같다.

$$\begin{aligned} T(n) &= T({n\over2})+C(1) \\ &=T({n\over2^2})+2C(1) \\ &= ... \\ &=T({n\over2^k})+kC(1) \\ {n\over2^k}&=1 \\ n&=2^k \\ k&=log(n) \\ &∴O(log(n)) \\ &C(1)은 상수시간 이므로 \end{aligned}$$

---

행렬의 거듭제곱

n*n 행렬이 주어질 때 행렬을 여러번 거듭제곱하는 문제다.

행렬의 곱셈에는 $O(n^3)$만큼의 시간이 걸리므로 지수부분을 1씩 감소시키면서 거듭제곱을 하면 시간이 매우 오래 걸린다.

$A^m$의 시간 복잡도는 $O(n^3m)$으로 매우 오래 걸리는 것을 알 수 있다.

이를 분할정복을 이용하여 계산해보자

문제를 반으로 나눠보기

거듭제곱은 다음 처럼 나타낼 수 있다.

$$A^m=A^{m/2}*A^{m/2}$$

$A^{m/2}$를 한 번 구하면 다른 하나는 추가로 계산할 필요가 없으므로 시간이 단축될 것이다.

코드로 구현하기

코드로 구현하면 다음과 같다.

// size 크기의 항등행렬 반환하는 메소드
static int[][] identityMatrix(int size) {
    int matrix[][] = new int[size][size];

    for (int i = 0; i < size; i++) {
        matrix[i][i] = 1;
    }

    return matrix;
}

// 두 행렬을 곱하는 메소드
static int[][] multiplyMatrix(int[][] aMatrix, int[][] bMatrix) {
    int[][] resultMatrix = new int[aMatrix.length][aMatrix.length];

    // 두 행렬의 곱
    for (int i = 0; i < aMatrix.length; i++) {
        for (int j = 0; j < aMatrix.length; j++) {
            int sum = 0;

            for (int k = 0; k < aMatrix.length; k++) {
                int tmp = (aMatrix[i][k] * bMatrix[k][j]);
                sum += tmp;
            }

            resultMatrix[i][j] = sum;
        }
    }

    return resultMatrix;
}

// matrix 행렬을 m제곱한 값을 반환하는 메소드
static int[][] matrixPow(int[][] matrix, int m) {
    if (m == 0) {
        return identityMatrix(matrix.length);
    }

    // m이 홀수인 경우
    if (m % 2 != 0) {
        return multiplyMatrix(matrix, matrixPow(matrix, m - 1));
    }

    // 문제를 반으로 나누기
    int halfMatrix[][] = matrixPow(matrix, m / 2);

    // 제곱하기
    return multiplyMatrix(halfMatrix, halfMatrix);
}

---

---

---

Uploaded by N2T