이진 검색 트리

1. 이진 검색 트리란?

💡

자료들을 일정한 순서에 따라 정렬한 상태로 저장해두는 트리

사용 예시

• 캐릭터 생성 시 특정 닉네임이 이미 저장되어있는지 확인하기

• 나보다 1등 위인 사람과 1등 아래인 사람을 찾기

대부분 언어 표준 라이브러리에서 제공하기 때문에, 직접 구현하지 않는다.

---

2. 이진 검색 트리의 정의와 조작

2-1. 이진트리란?

💡

한 노드당 최대 2개의 자식 노드만 가질 수 있는 트리

따라서 관련 객체 작성 시 다음처럼 구현이 된다.

class Node {
    int data;
    Node left, right;
}

2-2. 이진 검색 트리의 특징

• N개의 원소 중에서 원하는 원소를 찾기까지 걸리는 시간은 다음과 같다.

$$O(\log{N})$$

시간이 logN이 걸리기 위해선 노드들이 특별한 방식으로 저장될 필요가 있다.

특별한 방식으로 저장된 이진 트리

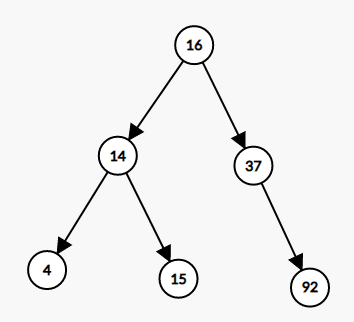
위 트리를 보면, 한 노드 기준으로 왼쪽은 작은 자식, 오른쪽은 큰 자식을 가진다.

2-3. 오름차, 내림차 순회 방법

• 가장 왼쪽에 있는 자식이 항상 가장 작은 값을 가진다.

• 가장 오른쪽에 있는 자식이 항상 가장 큰 값을 가진다.

오름차 순회방법

• (왼쪽-자신-오른쪽) 중위 순회를 한다.

내림차 순회방법

• (오른쪽-자신-왼쪽) 중위 순회를 한다.

2-4. 자료의 검색 방법

이진 탐색하고 유사한 방식으로 동작한다.

[0,5] → mid = (0+5)//2 = 2

[0,2] → mid = (0+2)//2 = 1

0	1	2	3	4
1	3	5	7	9

특별한 방식으로 저장된 이진 트리

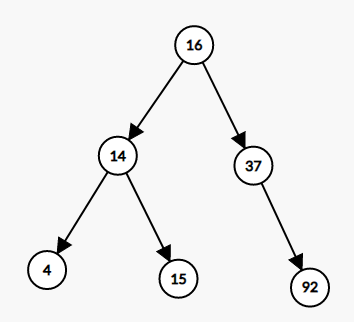
위 트리에서 15를 찾고 싶다고 해보자.

루트(16)부터 시작해서 15는 더 작은 값이므로, 왼쪽

다음 노드(14)는 더 큰 값이므로, 오른쪽

15값을 찾게 된다.

한 번 원소를 비교할 때 마다 비교 대상이 절반이 되므로 빠른 속도로 탐색이 가능하다.

2-5. 근데 그럴바에 그냥 배열가져다 쓰지 왜 이진 검색 트리 씀?

배열의 삽입 삭제가 어렵다는 단점을 해결할 수 있다.

삽입

위 트리에서 38이라는 값을 넣고 싶다고 하자.

루트부터 탐색 연산이 이루어진다.

• 루트(31)보다 크므로 오른쪽 자식으로 넘어간다.

• 다음 노드(72)보다 작으므로 왼쪽 자식으로 넘어간다.

• 다음 노드(55)보다 작으므로 왼쪽 자식으로 넘어간다.

• 다음 노드(49)보다 작으므로 왼쪽 자식으로 넘어간다.

• 현재 위치는 Null이므로 현재 위치에 추가한다.

삭제

삭제연산은 삽입연산보다 약간 까다롭다.

다음과 같은 노드에서 72값을 가진 노드를 제거한다고 해보자.

72값을 가지는 노드의 서브트리 2개를 살펴보자

1. 두 서브트리만으로 합쳐진 하나의 트리를 만든다.

2. 이후, 72노드의 위치에 끼워넣으면 72는 자연스레 제거가된다.

---

3. 시간 복잡도 분석과 균형 잡힌 이진 검색 트리

최대 재귀 호출의 수는 트리의 높이와 같다. 따라서 시간 복잡도는 다음과 같다.

$$O(h)$$

하지만, 위와 같은 이진 검색 트리를 만들기 위해서 1~100까지 숫자를 오름차순으로 삽입했다고 해보자.

그럼 트리는 다음과 같은것이다.

위와 같은 트리를 Skewed Tree 라고 한다.

이렇게 되면, 이진 검색 트리의 이점이 사라지게 된다.

문제를 해결하기 위한 균형 잡힌 이진 검색 트리

이를 해결하기 위해 레드-블랙 트리를 사용한다.

대부분의 표준 라이브러리에도 레드-블랙 트리로 구현되어있다.

---

4. 균형 잡힌 이진 검색 트리 직접 구현하기: 트립

💡

기존 이진트리의 단점을 보완하기 위한 방법

• 기존 이진트리는 X보다 작은 원소의 수를 계산하거나, k번째 원소를 찾는 연산을 지원하지 않는다.

• 이를 해결하기 위한 방법으로 AVL, Red-Black, treap이 있다. 그 중에서 구현이 가장 쉬운 treap을 사용한다.

Treap이란?

💡

랜덤화된 이진트리

• 트리의 형태가 원소들의 추가 순서에 따라 결정되지 않고, 난수에 의해 임의대로 결정된다.

• 트리 높이의 기대치는 항상 일정하다.

• 노드 마다 우선순위(난수)를 부여한다.

• 트립은 항상 부모의 우선순위가 자식의 우선순위보다 높은 이진 검색 트리를 만든다.

트리의 높이

난수인데 어떻게 높이가 lgN일수가 있는가?

→ 트리의 높이 기대값이 O(lgN)임을 증명해보자.

증명

• N개의 노드로 이루어진 트리가 있다고 해보자.

• 루트는 r번째로 작은 원소를 가진다면 다음이 성립한다.
  • 루트 왼쪽에는 r-1개의 원소
  • 루트 오른쪽에는 N-r개의 원소

• 각 확률을 계산해보자
  • 우리가 찾고자 하는 노드가 왼쪽에 있을 확률은 다음과 같다.

    $$찾고자\ 하는\ 노드가\ 왼쪽에\ 있을\ 확률={(r-1)\over N}$$

  • 우리가 찾고자 하는 노드가 루트에 있을 확률은 다음과 같다.

    $$찾고자\ 하는\ 노드가\ 루트에\ 있을\ 확률={1\over N}$$

  • 우리가 찾고자 하는 노드가 오른쪽에 있을 확률은 다음과 같다.

    $$찾고자\ 하는\ 노드가\ 루트에\ 있을\ 확률={(N-r)\over N}$$

• 다음 단계에서의 기대값을 구해보자
  • 기댓값 공식은 다음과 같다.

    $$E[X] = \sum_{i=1}^{n}x_iP(x_i)$$

  • 위 공식을 이용해서 기대값을 계산하면 다음과 같다.

    $$(r-1)*{r-1\over N} + 1*{1\over N}+(N-r)*{N-r \over N}={(r-1)^2+1^2+(N-r)^2\over N}$$

• 1부터 N까지 모든 r의 출현 확률이 같다고 가정하자. 이제 모든 r에 대한 값의 평균을 취해보자

  $${1 \over N}\sum_{r=1}^N{(r-1)^2+1^2+(N-r)^2\over N}$$

  • 위 식을 정리하면 다음과 같다.

  $${2N^2-3N+4\over 3N} \approx {2\over3}N$$

• 즉 한 단계가 내려갈 때 마다 후보의 수가 2/3씩 줄어든다는 뜻이다.

• 따라서 O(lgN) 단계를 거치면 답을 찾을 수 있다.

---

Uploaded by N2T