동적 계획법이 뭔데?
분할 정복에서 중복 부분문제를 캐시(cache)를 이용하여 계산 결과를 재활용하여 속도 향상을 꾀하는 기법이다.
예시
피보나치 수열의 [i]번째 결과값을 출력하고싶다고 하자.
해당 메소드는 fibo(i)를 이용하여 값을 얻는다.
int fibo(int i){
// 기저사례
if(i == 0 || i == 1){
return 1;
}
if(cache[i] != -1){
return cache[i];
}
cache[i] = fibo(i-1) + fibo(i-2);
return cache[i];
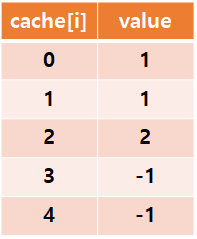
}- 초기 cache 상태는 다음과 같다.

- fibo(4)는 fibo(3) + fibo(2) 연산이 이루어진다.

- fibo(3)에서는 fibo(2) + fibo(1) 연산이 이루어진다.
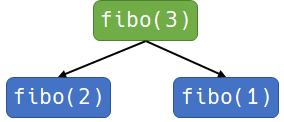
- fibo(2)에서는 fibo(1) + fibo(0) 연산이 이루어진다.
fibo(1) = 1, fibo(0) = 1 이므로 fibo(2) 값은 2를 반환하며 cache[2]에 값을 저장한다.

- fibo(3) 연산으로 다시 올아와서 fibo(2)는 추가적인 연산 없이 cache[2]값을 가져와서 처리한다.
이 때 cache[3]에 fibo(2) + fibo(1) 값을 저장한다.


- 마지막으로 fibo(4) 연산으로 돌아와서 fibo(3) + fibo(2)를 처리한다.
이 둘은 이미 캐시에 존재하므로 마찬가지로 캐시를 이용하여 계산한다.
fibo(4)의 결과값을 cache[4]에 저장한다.


i값이 작기 때문에 와닿지 않을 수 있다.
이를 기존 fibo코드와 비교하며 시간복잡도를 구해보자
int fibo2(int i){
if(i == 1 || i == 0){
return 1;
}
return fibo2(i-1) + fibo(i-2);
}한 번 호출할 때 마다 2번의 fibo2가 호출되므로, 시간복잡도는 O(n^2)다.
하지만 동적 계획법을 사용한다면 중복 연산이 없어지므로 O(n)만에 해결할 수 있다.
구현 패턴
패턴을 이용하여 구현을 하면 작성이 편하고, 버그를 찾기도 유용하다.
다음 재귀함수가 있다고 해보자
// a와 b는 각각 [0,2500) 구간 안의 정수
// 반환 값은 항상 int형 안에 들어가는 음이 아닌 정수
int someObscureFunction(int a, int b);항상 기저 사례를 가장 먼저 처리한다.- 입력이 범위를 벗어난 경우
- 피보나치 수열의 경우 [0], [1] 은 1값을 가진다.
함수의 반환값이 항상 0 이상이기 때문에 cache[]를 모두 -1로 초기화하지만 반환값이 음수가 될 수 있다면 이 방법은 쓸 수 없다.
cache를 쉽게 초기화하는 방법JAVA의 경우 Arrays.fill(array, value); 를 이용하여 array에 있는 1차원 배열을 value값으로 초기화해준다.
다음 패턴으로 구성된 의사코드를 보자
// 전부 -1로 초기화해 둔다
int cache[2500][2500];
// a와 b는 각각 [0,2500) 구간 안의 정수
// 반환 값은 항상 int형 안에 들어가는 음이 아닌 정수
int someObscureFunction(int a, int b){
// 기저 사례를 처음에 처리한다.
if(...) return;
// (a,b)에 대한 답을 구한 적이 있으면 곧장 반환
if(cache[a][b] != -1){
return cache[a][b];
}
// 여기에서 답을 계산
...
return cache[a][b];
}
public static void main(String[] args){
// Arrays.fill을 이용해 1차원 배열 초기화
for(int i=0;i<cache.length();i++){
Arrays.fill(cache[i],-1);
}
}동적 계획법 레시피
- 주어진 문제를 완전 탐색을 이용해 해결한다.
- 중복된 부분 문제를 한 번만 계산하도록 메모이제이션을 적용한다.
최적화 문제 동적 계획법 레시피
- 모든 답을 만들어보고 최적해의 점수를 반환하는 완전 탐색 알고리즘을 설계한다.
- 앞으로 남은 선택들에 해당하는 점수만을 반환하도록 부분 문제 정의를 바꾼다.
- 이전 선택에 관련된 정보가 있다면 꼭 필요한 것만 남기고 줄인다.
중복 부분 문제를 최대한 많이 만들어라
- 입력이 배열이거나 문자열인 경우 적절한 변환을 통해 메모이제이션을 할 수있도록 하라
- 메모이제이션을 적용하라
Uploaded by N2T
'Algorithm > 알고리즘 (기초)' 카테고리의 다른 글
| 벨판-포드의 최단 경로 알고리즘 (0) | 2023.02.09 |
|---|---|
| 이진 검색 트리 (0) | 2023.02.01 |
| 3.4 MANIPULATING BIG-O (0) | 2021.10.04 |
| 3.1 RANK THE FUNCTIONS (0) | 2021.10.04 |
| 2.7 FIBONACCI NUMBERS (0) | 2021.10.04 |
