용어 정리
- |S|
- 문자열 S의 길이
- S = “abcde” 라면 |S| = 5
- S[i] (0 ≤ i < |S|)
- 문자열 S의 i번 글자
- S = “abcde” 라면 S[3] = d
- S[i…j]
- 문자열 S[i] 부터 S[j] 까지 부분 문자열
- S = “abcde” 라면 S[1…3] = bcd
- S[…a]
- 문자열 S[0] 부터 S[a] 까지 부분 문자열
- S = “abcde” 라면 S[…3] = abcd
- S[b…]
- 문자열 S[b] 부터 S[|S|-1] 까지 부분 문자열
- S = “abcde” 라면 S[3…] = de
문자열 검색
긴 문자열 H가 문자열 N을 부분 문자열로 포함하는지 확인하는 방법
H = “avava” N = “ava” 라면 N이 출현하는 모든 인덱스를 반환하는 알고리즘을 작성한다고 하자
이때 결과값은 0, 2이다.
가장 간단한 방법
N의 가능한 모든 시작 위치를 다 시도해보는 것이다.
다음은 JAVA 코드이다.
import java.util.ArrayList;
import java.util.List;
public class 단순한_문자열_검색_알고리즘_구현 {
// H의 부분 문자열로 N이 출현하는 시작위치들을 모두 반환한다.
public static List<Integer> naiveSearch(String H, String N) {
List<Integer> result = new ArrayList<>();
// 모든 시작 위치를 다 시도해 본다.
for (int begin = 0; begin + N.length() <= H.length(); begin++) {
boolean matched = true;
// N문자열이 H의 begin 인덱스부터 전부 들어가는 지 체크
for (int i = 0; i < N.length(); i++) {
if (H.charAt(begin + i) != N.charAt(i)) {
matched = false;
break;
}
}
if (matched) {
result.add(begin);
}
}
return result;
}
public static void main(String[] args) {
}
}
해당 알고리즘을 그림으로 표현하면 다음과 같다.
해당 인덱스의 문자 불일치가 발생하면 바로 다음 인덱스부터 시작한다.
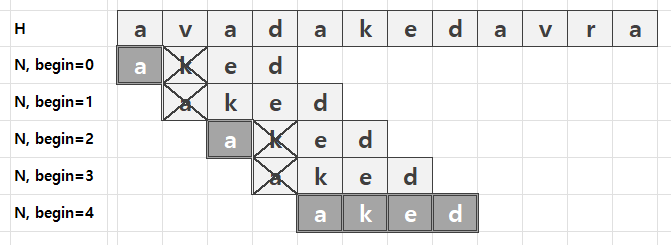
입력이 큰 경우에는 비효율적이지만, 구현이 단순하다는 장점 때문에 표준 라이브러리로 사용된다.
- C : strstr()
- C++ : string::find()
- JAVA : indexOf()
KMP(Knuth-Morris-Pratt) 알고리즘
검색 과정에서 얻은 정보를 이용하여 불필요한 탐색을 줄이는 방법이다.
어떤 긴 문자열에서 N = “aabaabac”를 찾는다고 해보자.
시작 위치 i부터 N을 맞춰 보니 첫 7글자 “aabaaba”는 서로 일치했지만 마지막 문자 ‘c’에서 불일치가 발생했다.
위에서 학습한 단순 알고리즘이라면 i+1부터 시작하겠지만, 위 정보를 바탕으로 불필요한 탐색을 줄여보도록 하자.

위 그림을 보면 i+1에서 시작하는 N은 정답이 될 수 없다. 결국 이를 찾다보면 정답이 될 가능성이 있는 begin은 i+3과 i+6 밖에 없다.
따라서 i를 1씩 증가시키느 것이 아닌 i+3과 i+6만 처리하면 된다.
그래서 시작 위치를 어떻게 찾는데?
우리가 아는 정보는 이전 부분 문자열의 시작 위치, 이전 부분 문자열의 일치하는 문자 수 를 알고있다.
위 그림에서 7글자가 일치하고 다음 글자가 불일치 함을 알 수 있다.
이 때 7글자가 일치했기 때문에, N의 접두사 N[i…7-1]가 H[i…i+7-1]와 일치했음을 알 수 있다.
시작 위치 i+k에서 답을 찾기 위해서 N[…7-1]의 길이 7-k인 접두사와 접미사가 같아야 한다.
따라서 N의 각 접두사에 대해 접두사도 되고 접미사도 되는 문자열의 최대 길이를 계산하면 된다.
접두사도 되고, 접미사도 되는 문자열이 “aaba”, “a” 두가지가 있다. “aaba”를 이용해서 3만큼 이동이 가능하다.
다음을 정의하자
pi[i] = N[…i]의 접두사도 되고 접미사도 되는 문자열의 최대 길이
예를들어 알아보자
N = “aabaabac” 일 때 부분 일치 테이블의 계산
i N[…i] 접두사이면서 접미사인 최대 문자열 pi[i]
| 0 | a | (없음) | 0 |
| 1 | aa | a | 1 |
| 2 | aab | (없음) | 0 |
| 3 | aaba | a | 1 |
| 4 | aabaa | aa | 2 |
| 5 | aabaab | aab | 3 |
| 6 | aabaaba | aaba | 4 |
| 7 | aabaabac | (없음) | 0 |
matched 글자가 일치한 후 불일치가 발생한다면, 어디부터 시작해야 할까?
정답은 matched-pi[matched-1]만큼 증가시킨 위치이다.
위 표에선 7글자가 일치하므로, 7-pi[6] = 7-4 = 3
즉 3만큼의 인덱스를 증가시키면 된다.
상식적으로 생각해서 N의 aaba의 접두사와 접미사가 같고, 7글자까지 일치하므로, 뒤 4글자를 넘긴 인덱스만큼을 증가시킨다 라고 생각하면 된다.
알고리즘의 구현
static List<Integer> kmpSearch(String H, String N) {
List<Integer> result = new ArrayList<>();
// pi[i] = N[..i]의 접미사도 되고, 접두사도 되는 문자열의 최대 길이
List<Integer> pi = getPartialMatch(N);
// begin=matched=0 에서 시작
int begin = 0, matched = 0;
while (begin <= H.length() - N.length()) {
if (matched < N.length() && H.charAt(begin + matched) == N.charAt(matched)) {
matched++;
// N글자가 모두 일치했다면 답에 추가
if (matched == N.length()) {
result.add(begin);
}
} else {
// matched가 0인 경우에는 다음칸부터 계속
if (matched == 0) {
begin++;
} else {
begin += matched - pi.get(matched - 1);
// begin을 옮긴 후에 접두사는 이미 일치함
matched = pi.get(matched - 1);
}
}
}
return result;
}
시간 복잡도 분석
getPartialMatch()는 무시하고 계산해보자
문자 비교 연산은 각 문자당 한 번 씩 즉 O(|H|)번(begin을 옮긴 후에 접두사는 체크하지 않으므로) 수행된다.
항상 실패한다고 하면, begin은 0부터 |H|-|N|이 될 것이다. (시작 위치가 |H|-|N|을 초과하면 추가로 비교연산을 할 필요가 없다.)
따라서 연산 수행 횟수는 O(|H|)이다.
부분 일치 테이블 생성하기
단순한 문자열 알고리즘을 통해 부분 일치 테이블 생성하기
i = 접미사의 시작 인덱스
static List<Integer> getPartialMatchNaive(String N) {
List<Integer> pi = new ArrayList<>();
for (int i = 0; i < N.length(); i++) {
pi.add(0);
}
// i부터 시작하면서
for (int i = 1; i < N.length(); i++) {
// j+1글자가 일치한다.
for (int j = 0; i + j < N.length(); j++) {
if (N.charAt(i + j) != N.charAt(j)) {
break;
}
pi.set(i + j, Math.max(pi.get(i + j), j + 1));
}
}
System.out.println(pi);
return pi;
}
O(|N|^2)의 시간 복잡도를 가진다.
이 역시 KMP를 이용해서 구할 순 없을까?
KMP 알고리즘으로 부분 일치 테이블 생성하기
static List<Integer> getPartialMatch(String N) {
// pi[i] = N[..i]의 접미사도 되고, 접두사도 되는 문자열의 최대 길이
List<Integer> pi = new ArrayList<>();
for (int i = 0; i < N.length(); i++) {
pi.add(0);
}
// KMP로 자기 자신을 찾는다.
// N을 N에서 찾는다 begin=0은 처리 안함
int begin = 1, matched = 0;
// 비교할 문자가 N의 끝에 도달할 때 까지 찾으면서 부분 일치를 모두 기록한다.
while (begin + matched < N.length()) {
if (N.charAt(begin + matched) == N.charAt(matched)) {
matched++;
pi.set(begin + matched - 1, matched);
} else {
if (matched == 0) {
begin++;
} else {
begin += matched - pi.get(matched - 1);
matched = pi.get(matched - 1);
}
}
}
return pi;
}
왜 begin = 0은 처리를 안하는가?ㅁ
부분 문자열의 길이가 같을 때 ex] abcdefghijklmnop 의 길이의 문자가 있을 때 접두사, 접미사가 abcdefghijklmnop 인 녀석은 제외하기 위함
위 알고리즘 또한 KMP를 사용했으므로, 위에 계산한 시간 복잡도를 대입하여 O(|N|)이 됨을 알 수 있다.
따라서 총 시간 복잡도는 O(|N|+|H|)가 됨을 알 수 있다.
예제: 접두사/접미사 문제(난이도: 하)
긴 문자열 S가 주어질 때 이 문자열의 접두사도 되고 접미사도 되는 부분 문자열의 길이를 모두 출력하라.
S = “ababbaba” 라고 하자.
getPartialMatch를 통해 pi테이블을 만들 수 있다. 이를 통해 알 수 있는 것은 pi[7] = 3임을 알 수 있다. 하지만, “a” 또한 접두사이면서 접미사가 될 수 있다. 이는 어떻게 찾을 것인가?
pi[7]=3 정보를 살펴보자 이는 문자열 전체에서 3글자가 접두사이면서 접미사라는 뜻이다.
그러면 “aba”에서 공통 접두사, 접미사를 찾으면 되는 것이 아닌가?
pi[3]의 정보를 통해 공통 접두사, 접미사의 길이를 찾자.
예제: 팰린드롬 만들기 (난이도: 하)
문자열 S뒤에 적절한 문자열을 붙여서 가장 짧은 펠린드롬을 만들어라.
S의 접미사이면서 S`의 접두사를 찾아내자.
용어 정리
- |S|
- 문자열 S의 길이
- S = “abcde” 라면 |S| = 5
- S[i] (0 ≤ i < |S|)
- 문자열 S의 i번 글자
- S = “abcde” 라면 S[3] = d
- S[i…j]
- 문자열 S[i] 부터 S[j] 까지 부분 문자열
- S = “abcde” 라면 S[1…3] = bcd
- S[…a]
- 문자열 S[0] 부터 S[a] 까지 부분 문자열
- S = “abcde” 라면 S[…3] = abcd
- S[b…]
- 문자열 S[b] 부터 S[|S|-1] 까지 부분 문자열
- S = “abcde” 라면 S[3…] = de
문자열 검색
긴 문자열 H가 문자열 N을 부분 문자열로 포함하는지 확인하는 방법
H = “avava” N = “ava” 라면 N이 출현하는 모든 인덱스를 반환하는 알고리즘을 작성한다고 하자
이때 결과값은 0, 2이다.
가장 간단한 방법
N의 가능한 모든 시작 위치를 다 시도해보는 것이다.
다음은 JAVA 코드이다.
import java.util.ArrayList;
import java.util.List;
public class 단순한_문자열_검색_알고리즘_구현 {
// H의 부분 문자열로 N이 출현하는 시작위치들을 모두 반환한다.
public static List<Integer> naiveSearch(String H, String N) {
List<Integer> result = new ArrayList<>();
// 모든 시작 위치를 다 시도해 본다.
for (int begin = 0; begin + N.length() <= H.length(); begin++) {
boolean matched = true;
// N문자열이 H의 begin 인덱스부터 전부 들어가는 지 체크
for (int i = 0; i < N.length(); i++) {
if (H.charAt(begin + i) != N.charAt(i)) {
matched = false;
break;
}
}
if (matched) {
result.add(begin);
}
}
return result;
}
public static void main(String[] args) {
}
}
해당 알고리즘을 그림으로 표현하면 다음과 같다.
해당 인덱스의 문자 불일치가 발생하면 바로 다음 인덱스부터 시작한다.
입력이 큰 경우에는 비효율적이지만, 구현이 단순하다는 장점 때문에 표준 라이브러리로 사용된다.
- C : strstr()
- C++ : string::find()
- JAVA : indexOf()
KMP(Knuth-Morris-Pratt) 알고리즘
검색 과정에서 얻은 정보를 이용하여 불필요한 탐색을 줄이는 방법이다.
어떤 긴 문자열에서 N = “aabaabac”를 찾는다고 해보자.
시작 위치 i부터 N을 맞춰 보니 첫 7글자 “aabaaba”는 서로 일치했지만 마지막 문자 ‘c’에서 불일치가 발생했다.
위에서 학습한 단순 알고리즘이라면 i+1부터 시작하겠지만, 위 정보를 바탕으로 불필요한 탐색을 줄여보도록 하자.
위 그림을 보면 i+1에서 시작하는 N은 정답이 될 수 없다. 결국 이를 찾다보면 정답이 될 가능성이 있는 begin은 i+3과 i+6 밖에 없다.
따라서 i를 1씩 증가시키느 것이 아닌 i+3과 i+6만 처리하면 된다.
그래서 시작 위치를 어떻게 찾는데?
우리가 아는 정보는 이전 부분 문자열의 시작 위치, 이전 부분 문자열의 일치하는 문자 수 를 알고있다.
위 그림에서 7글자가 일치하고 다음 글자가 불일치 함을 알 수 있다.
이 때 7글자가 일치했기 때문에, N의 접두사 N[i…7-1]가 H[i…i+7-1]와 일치했음을 알 수 있다.
시작 위치 i+k에서 답을 찾기 위해서 N[…7-1]의 길이 7-k인 접두사와 접미사가 같아야 한다.
따라서 N의 각 접두사에 대해 접두사도 되고 접미사도 되는 문자열의 최대 길이를 계산하면 된다.
접두사도 되고, 접미사도 되는 문자열이 “aaba”, “a” 두가지가 있다. “aaba”를 이용해서 3만큼 이동이 가능하다.
다음을 정의하자
pi[i] = N[…i]의 접두사도 되고 접미사도 되는 문자열의 최대 길이
예를들어 알아보자
N = “aabaabac” 일 때 부분 일치 테이블의 계산
i N[…i] 접두사이면서 접미사인 최대 문자열 pi[i]
| 0 | a | (없음) | 0 |
| 1 | aa | a | 1 |
| 2 | aab | (없음) | 0 |
| 3 | aaba | a | 1 |
| 4 | aabaa | aa | 2 |
| 5 | aabaab | aab | 3 |
| 6 | aabaaba | aaba | 4 |
| 7 | aabaabac | (없음) | 0 |
matched 글자가 일치한 후 불일치가 발생한다면, 어디부터 시작해야 할까?
정답은 matched-pi[matched-1]만큼 증가시킨 위치이다.
위 표에선 7글자가 일치하므로, 7-pi[6] = 7-4 = 3
즉 3만큼의 인덱스를 증가시키면 된다.
상식적으로 생각해서 N의 aaba의 접두사와 접미사가 같고, 7글자까지 일치하므로, 뒤 4글자를 넘긴 인덱스만큼을 증가시킨다 라고 생각하면 된다.
알고리즘의 구현
static List<Integer> kmpSearch(String H, String N) {
List<Integer> result = new ArrayList<>();
// pi[i] = N[..i]의 접미사도 되고, 접두사도 되는 문자열의 최대 길이
List<Integer> pi = getPartialMatch(N);
// begin=matched=0 에서 시작
int begin = 0, matched = 0;
while (begin <= H.length() - N.length()) {
if (matched < N.length() && H.charAt(begin + matched) == N.charAt(matched)) {
matched++;
// N글자가 모두 일치했다면 답에 추가
if (matched == N.length()) {
result.add(begin);
}
} else {
// matched가 0인 경우에는 다음칸부터 계속
if (matched == 0) {
begin++;
} else {
begin += matched - pi.get(matched - 1);
// begin을 옮긴 후에 접두사는 이미 일치함
matched = pi.get(matched - 1);
}
}
}
return result;
}
시간 복잡도 분석
getPartialMatch()는 무시하고 계산해보자
문자 비교 연산은 각 문자당 한 번 씩 즉 O(|H|)번(begin을 옮긴 후에 접두사는 체크하지 않으므로) 수행된다.
항상 실패한다고 하면, begin은 0부터 |H|-|N|이 될 것이다. (시작 위치가 |H|-|N|을 초과하면 추가로 비교연산을 할 필요가 없다.)
따라서 연산 수행 횟수는 O(|H|)이다.
부분 일치 테이블 생성하기
단순한 문자열 알고리즘을 통해 부분 일치 테이블 생성하기
i = 접미사의 시작 인덱스
static List<Integer> getPartialMatchNaive(String N) {
List<Integer> pi = new ArrayList<>();
for (int i = 0; i < N.length(); i++) {
pi.add(0);
}
// i부터 시작하면서
for (int i = 1; i < N.length(); i++) {
// j+1글자가 일치한다.
for (int j = 0; i + j < N.length(); j++) {
if (N.charAt(i + j) != N.charAt(j)) {
break;
}
pi.set(i + j, Math.max(pi.get(i + j), j + 1));
}
}
System.out.println(pi);
return pi;
}
O(|N|^2)의 시간 복잡도를 가진다.
이 역시 KMP를 이용해서 구할 순 없을까?
KMP 알고리즘으로 부분 일치 테이블 생성하기
static List<Integer> getPartialMatch(String N) {
// pi[i] = N[..i]의 접미사도 되고, 접두사도 되는 문자열의 최대 길이
List<Integer> pi = new ArrayList<>();
for (int i = 0; i < N.length(); i++) {
pi.add(0);
}
// KMP로 자기 자신을 찾는다.
// N을 N에서 찾는다 begin=0은 처리 안함
int begin = 1, matched = 0;
// 비교할 문자가 N의 끝에 도달할 때 까지 찾으면서 부분 일치를 모두 기록한다.
while (begin + matched < N.length()) {
if (N.charAt(begin + matched) == N.charAt(matched)) {
matched++;
pi.set(begin + matched - 1, matched);
} else {
if (matched == 0) {
begin++;
} else {
begin += matched - pi.get(matched - 1);
matched = pi.get(matched - 1);
}
}
}
return pi;
}
왜 begin = 0은 처리를 안하는가?ㅁ
부분 문자열의 길이가 같을 때 ex] abcdefghijklmnop 의 길이의 문자가 있을 때 접두사, 접미사가 abcdefghijklmnop 인 녀석은 제외하기 위함
위 알고리즘 또한 KMP를 사용했으므로, 위에 계산한 시간 복잡도를 대입하여 O(|N|)이 됨을 알 수 있다.
따라서 총 시간 복잡도는 O(|N|+|H|)가 됨을 알 수 있다.
예제: 접두사/접미사 문제(난이도: 하)
긴 문자열 S가 주어질 때 이 문자열의 접두사도 되고 접미사도 되는 부분 문자열의 길이를 모두 출력하라.
S = “ababbaba” 라고 하자.
getPartialMatch를 통해 pi테이블을 만들 수 있다. 이를 통해 알 수 있는 것은 pi[7] = 3임을 알 수 있다. 하지만, “a” 또한 접두사이면서 접미사가 될 수 있다. 이는 어떻게 찾을 것인가?
pi[7]=3 정보를 살펴보자 이는 문자열 전체에서 3글자가 접두사이면서 접미사라는 뜻이다.
그러면 “aba”에서 공통 접두사, 접미사를 찾으면 되는 것이 아닌가?
pi[3]의 정보를 통해 공통 접두사, 접미사의 길이를 찾자.
예제: 팰린드롬 만들기 (난이도: 하)
문자열 S뒤에 적절한 문자열을 붙여서 가장 짧은 펠린드롬을 만들어라.
S의 접미사이면서 S`의 접두사를 찾아내자.
'Algorithm > 알고리즘 (Java)' 카테고리의 다른 글
| [Java] BFS : 너비 우선 탐색 (0) | 2021.12.05 |
|---|---|
| [Java] DFS : 깊이 우선 탐색 (0) | 2021.12.01 |
| [Java] 트라이(Trie) 알고리즘 (0) | 2021.11.16 |
| [Java] 프림 최소 스패닝 트리 (0) | 2021.11.15 |
| [Java] 상호 배타적 집합 (0) | 2021.09.23 |
